Articulación de cadera
(Diferencia entre revisiones)
| Revisión de 13:12 30 mar 2008 Edu (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:46 30 mar 2008 Mastromec (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 57: | Línea 57: | ||
| --[[Usuario:Edu|Edu]] 10:12 30 mar 2008 (ART) | --[[Usuario:Edu|Edu]] 10:12 30 mar 2008 (ART) | ||
| ---- | ---- | ||
| + | |||
| + | No hablo mas, VOY a dibujar para que se entienda, pero lo que propongo les va a gustar, solo que van a tener que agregar algunos senos en la interpolación. | ||
| + | por favor denme un tiempo. | ||
| + | |||
| + | --[[Usuario:Mastromec|Mastromec]] 10:46 30 mar 2008 (ART) | ||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
Revisión de 13:46 30 mar 2008
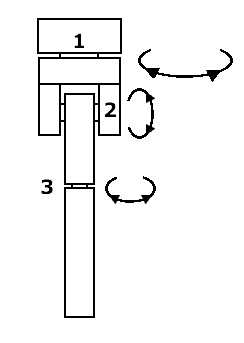
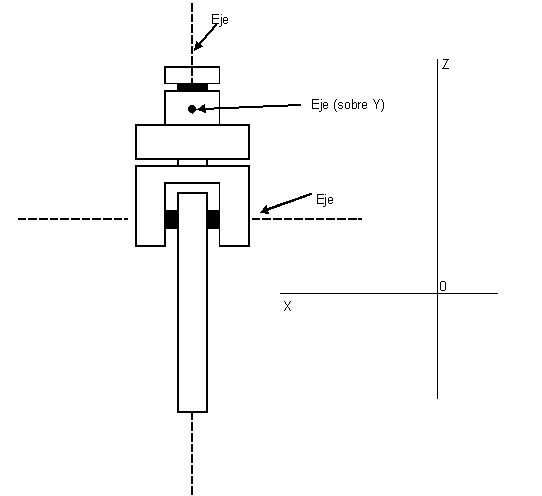
La articulación de cadera debería ser de 3 grados de libertad
- 1. Rotación en el eje vertical donde se une al cuerpo, unos 10 grados. Requeriría mucha fuerza.
- 2. Rotación para levantar la rodilla (eje horizontal ubicado en dirección derecha-izquierda), rota más de 90º y requerirá mucha fuerza.
- 3. Rotación del miembro (muslo) sobre su articulación (muy leve, unos 5 - 10º, incluso menos). No sé si será necesaria...
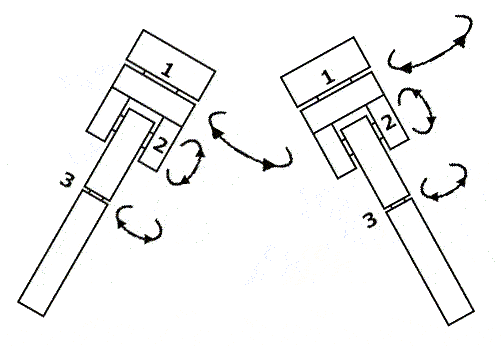
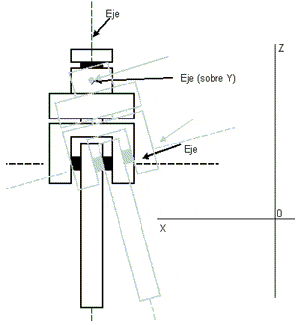
Aqui tengo algunas diferencias con vos Edu, no nos vamos a pelear, pero veo diferente los ejes. Para los modulos de control es mas simple si seguis con ejes ortogonales (creo) pero podrias controlar ejes que no sean ortogonales? Fijate en el esqueleto que la direccion del eje de la pierna es mas parecida a los antiguos muñecos de plastico.
Todavia no tengo elementos para mostrar lo que digo, por el momento tomalo como un comentario para análisis.
--Mastromec 18:12 29 mar 2008 (ART)
¿Estás pensando en rótulas esféricas? Eso necesitaría actuadores hidráulicos (lineales), com motores lo veo muy complicado. Además, me baso en lo que veo en ASIMO. Como dije antes, si llevan 20 años de investigación no creo que sea capricho lo que están usando.
--Edu 20:29 29 mar 2008 (ART)
No pense en rotulas porque me parece complicado el control, habria que trabajarlo mucho al tema y no creo que dispongamos de tanto tiempo. simplemente hable de diferentes direcciones, fijate que nuestro cuerpo no es "ortogonal" y los movimientos que estamos generando son ortogonales, (alineados siempre con ejes x,y,z) lo que pregunto es: que tan complicado se hace el control si tengo un eje en una direccion diferente?
Yo entiendo que en el control vos haces una interpolación (es correcto?) y corregis los datos para que el punto en cuestión se mueva. En la interpolacion correspondería ingresar un angulo constante en uno de los ejes, no se si se pueda, y no se si se entienda lo que digo.
con respecto al uso de rotulas, estas permiten las libertades elasticas, no intervienen en los movimientos controlados, solo dejan la posibilidad de mas combinaciones en el espacio
--Mastromec 20:54 29 mar 2008 (ART)
Juan, hablás de algo así, supongo.
Por mi parte yo creo que es algo así.
...se está complicando esto... :) me parece que llega la hora de comprar maderas, tuercas, arandelas y varillas roscadas.
--Adrian S.A. 01:04 30 mar 2008 (ART)
Juan, por qué no hacés un diagrama de lo que visualizás para la articulación de la cadera. Yo estoy completamente perdido.
Me parece que el tema no es agregar más ejes. Lo que hay que hacer, si son articulaciones más complejas que lo que estuvimos viendo, dividir sus movimientos en dos articulaciones. En forma teórica o en forma física, esto no cambia nada, en verdad.
Si es como supone Andrés en el dibujo, podemos pensar que arriba hay una articulación de dos grados de libertad que aporta el movimento que pone en diagonal la pierna y otra que aporta el giro marcado como 1 en mi dibujo.
Unida a ésa, abajo, está una articulación de dos grados de libertad que aporta los movimientos 2 y 3 (insisto que yo creo que el 3 no es necesario. Incluso que podemos encarar el diseño sin este movimiento, porque luego agregarlo no es tan difícil).
Si lo que está diciendo es otra cosa, perdón. Ya dije que mi capacidad de visualizar mecánica en teoría es muy pobre.
--Edu 10:12 30 mar 2008 (ART)
No hablo mas, VOY a dibujar para que se entienda, pero lo que propongo les va a gustar, solo que van a tener que agregar algunos senos en la interpolación. por favor denme un tiempo.
--Mastromec 10:46 30 mar 2008 (ART)
Relacionados:
- Piernas
- Caderas
- Rodillas
- Tibias
- Pies
- Articulaciones
- Articulación de cadera
- Articulación de rodilla
- Articulación del pie