Articulación de cadera
(Diferencia entre revisiones)
| Revisión de 20:49 25 abr 2008 Mastromec (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 01:38 26 abr 2008 Edu (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 148: | Línea 148: | ||
| + | --[[Usuario:Mastromec|Mastromec]] 17:49 25 abr 2008 (ART) | ||
| ---- | ---- | ||
| - | --[[Usuario:Mastromec|Mastromec]] 17:49 25 abr 2008 (ART) | ||
| - | |||
| - | |||
| + | Hola, aquí Edu. ¿Los círculos indican --su centro-- un punto de giro, verdad? Ayudame con esto, que para mecánica e interpretación de planos no soy muy bueno... | ||
| + | --[[Usuario:Edu|Edu]] 22:38 25 abr 2008 (ART) | ||
| + | ---- | ||
Revisión de 01:38 26 abr 2008
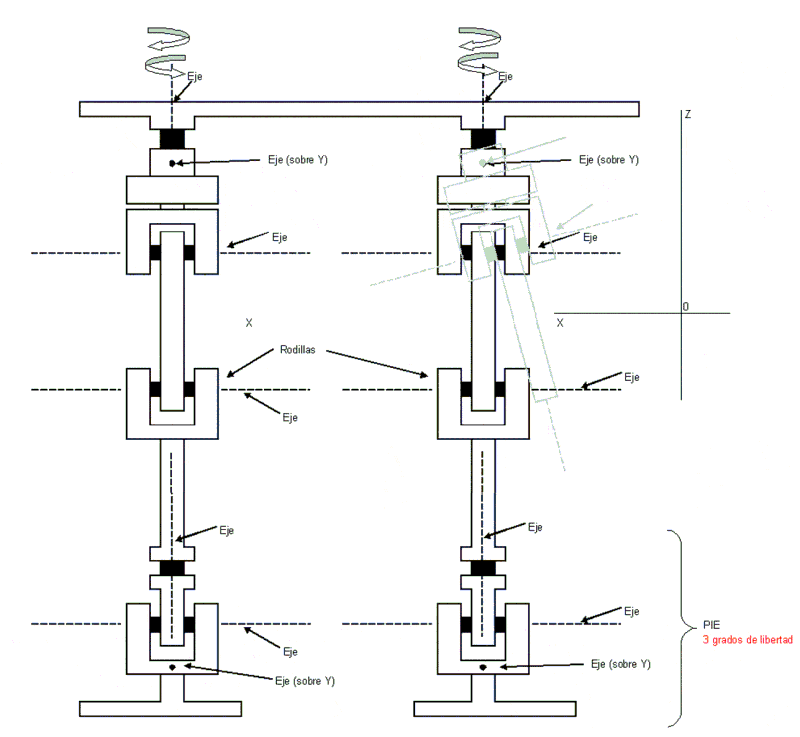
La articulación de cadera debería ser de 3 grados de libertad
- 1. Rotación en el eje vertical donde se une al cuerpo, unos 10 grados. Requeriría mucha fuerza.
- 2. Rotación para levantar la rodilla (eje horizontal ubicado en dirección derecha-izquierda), rota más de 90º y requerirá mucha fuerza.
- 3. Rotación del miembro (muslo) sobre su articulación (muy leve, unos 5 - 10º, incluso menos). No sé si será necesaria...
Aqui tengo algunas diferencias con vos Edu, no nos vamos a pelear, pero veo diferente los ejes. Para los modulos de control es mas simple si seguis con ejes ortogonales (creo) pero podrias controlar ejes que no sean ortogonales? Fijate en el esqueleto que la direccion del eje de la pierna es mas parecida a los antiguos muñecos de plastico.
Todavia no tengo elementos para mostrar lo que digo, por el momento tomalo como un comentario para análisis.
--Mastromec 18:12 29 mar 2008 (ART)
¿Estás pensando en rótulas esféricas? Eso necesitaría actuadores hidráulicos (lineales), com motores lo veo muy complicado. Además, me baso en lo que veo en ASIMO. Como dije antes, si llevan 20 años de investigación no creo que sea capricho lo que están usando.
--Edu 20:29 29 mar 2008 (ART)
No pense en rotulas porque me parece complicado el control, habria que trabajarlo mucho al tema y no creo que dispongamos de tanto tiempo. simplemente hable de diferentes direcciones, fijate que nuestro cuerpo no es "ortogonal" y los movimientos que estamos generando son ortogonales, (alineados siempre con ejes x,y,z) lo que pregunto es: que tan complicado se hace el control si tengo un eje en una direccion diferente?
Yo entiendo que en el control vos haces una interpolación (es correcto?) y corregis los datos para que el punto en cuestión se mueva. En la interpolacion correspondería ingresar un angulo constante en uno de los ejes, no se si se pueda, y no se si se entienda lo que digo.
con respecto al uso de rotulas, estas permiten las libertades elasticas, no intervienen en los movimientos controlados, solo dejan la posibilidad de mas combinaciones en el espacio
--Mastromec 20:54 29 mar 2008 (ART)
Juan, hablás de algo así, supongo.
Por mi parte yo creo que es algo así.
...se está complicando esto... :) me parece que llega la hora de comprar maderas, tuercas, arandelas y varillas roscadas.
--Adrian S.A. 01:04 30 mar 2008 (ART)
Juan, por qué no hacés un diagrama de lo que visualizás para la articulación de la cadera. Yo estoy completamente perdido.
Me parece que el tema no es agregar más ejes. Lo que hay que hacer, si son articulaciones más complejas que lo que estuvimos viendo, dividir sus movimientos en dos articulaciones. En forma teórica o en forma física, esto no cambia nada, en verdad.
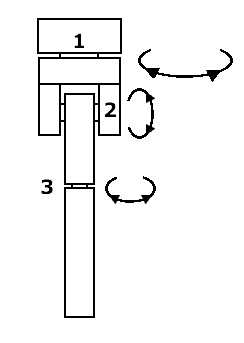
Si es como supone Adrián en el dibujo, podemos pensar que arriba hay una articulación de dos grados de libertad que aporta el movimento que pone en diagonal la pierna y otra que aporta el giro marcado como 1 en mi dibujo.
Unida a ésa, abajo, está una articulación de dos grados de libertad que aporta los movimientos 2 y 3 (insisto que yo creo que el 3 no es necesario. Incluso que podemos encarar el diseño sin este movimiento, porque luego agregarlo no es tan difícil).
Si lo que está diciendo es otra cosa, perdón. Ya dije que mi capacidad de visualizar mecánica en teoría es muy pobre.
--Edu 10:12 30 mar 2008 (ART)
No hablo mas, VOY a dibujar para que se entienda, pero lo que propongo les va a gustar, solo que van a tener que agregar algunos senos en la interpolación. por favor denme un tiempo.
--Mastromec 10:46 30 mar 2008 (ART)
¿Podremos ser capaces de mantener el equilibrio de este sistema mecánico? En modo "parado".
Sobre esa pelvis que une las dos piernas pondríamos una batería. Esto es un poco lo que proponía Eduardo al principio, lo de comenzar solo con un par de piernas. El pie hay que trabajarlo a la manera de Juan.
--Adrian S.A. 22:35 30 mar 2008 (ART)
No estaría mal. Se podría hacer con madera terciada y servos, a escala 50%, y nos permitiría ir probando programas y otras cosas...
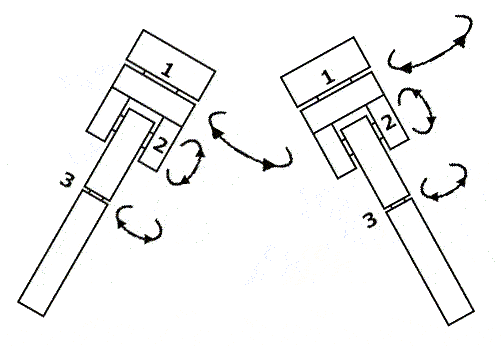
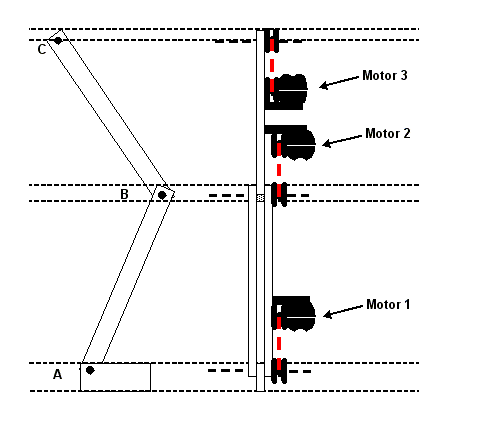
Este otro sistema es una especie de "pierna", a la izq. vista de perfil y a la derecha vista de frente.
Las líneas en rojo son correas tomadas a un motor por cada una de las 3 uniones mecánicas o articulaciones.
La idea es, prescindiendo del motor 3 para este experimento, lograr el comportamiento de un resorte de todo el conjunto cuando uno empuja aplicando una fuerza en el punto C en la dirección del punto A. Esto deberá hacer que C se acerque a A.
Cuando dejemos de presionar en C, el sistema deberá volver al estado anterior. ¿Qué necesitariamos para emular el comporamiento de un resorte en este sistema?.
Lograr un algoritmo para emular el comportamiento de un resorte creo que nos seviría. Los motores involucrados serían el 1 y el 2. ¿Qué opinan?.
(No critiquen los dibujos, que están hechos a las apuradas)
--Adrian S.A. 23:17 31 mar 2008 (ART)
Bueno, los ultimos dias aporte muy poco, estoy mudando mi oficina a un lugar mas amplio y por momentos estoy sin PC, espero me disculpen mis "desapariciones" temporarias.
Analicé bastante el tema de la cadera, como un sistema de mecanismos independientes trabajando juntos, la conclusion mas importante que llegue, es que estamos pensados para caminar hacia adelante, por este motivo inclui los angulos "raros" que ven en las imagenes.
Otra conclusion es que la apertura de las piernas en la direccion de la linea del camino (separación segun x) es variable con la velocidad del paso, y una tercera pero no menos importante es que la direccion del CG es la bisectriz del angulo formado por el camino y la direccion de cada pierna. (todas son discutibles por supuesto)
La idea que paso es solo eso, se que es mas complicado el control y trabajaremos en funcion de eso simplificando los movimientos, de todos modos se los puedo dar escritos como funciones.
El movimiento de la "rodilla" es un arco amplio, con un maximo en la mitad del recorrido angular. En la union pienso agregarle la posibilidad de abrir las piernas.
--Mastromec 21:39 6 abr 2008 (ART)
Fíjense que la columna vertebral no está alineada con las piernas. Es paralela.

--Adrian S.A. 22:10 6 abr 2008 (ART)
Es asi casi paralela, pero ademas en la posicion parado el femur tiene una inclinacion hacia atras, "llevando" el CG mas hacia el centro del area cubierta por los pies.
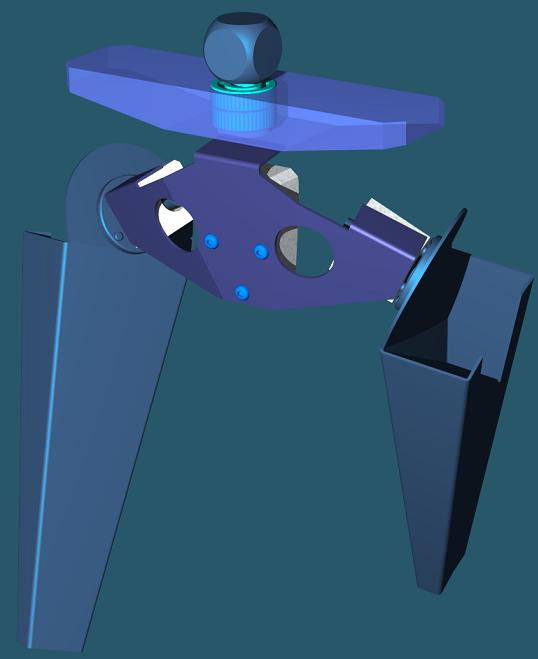
La foto que pusiste esta buena, yo use una parecida para darle el angulo entre la parte del femur que tiene la rotula y la parte "larga", el angulo esta indicado en las proporciones.
--Mastromec 22:40 6 abr 2008 (ART)
Aqui una animacion con angulos mas moderados, pero se verifica lo que en un principio comente, los angulos generan un movimiento mas suave. la animacion es mala, pero se entiende, equivoque los angulos y la deje asi nomas.
--Mastromec 21:30 8 abr 2008 (ART)
Me disculpo por la ausencia, es porque mude de oficina
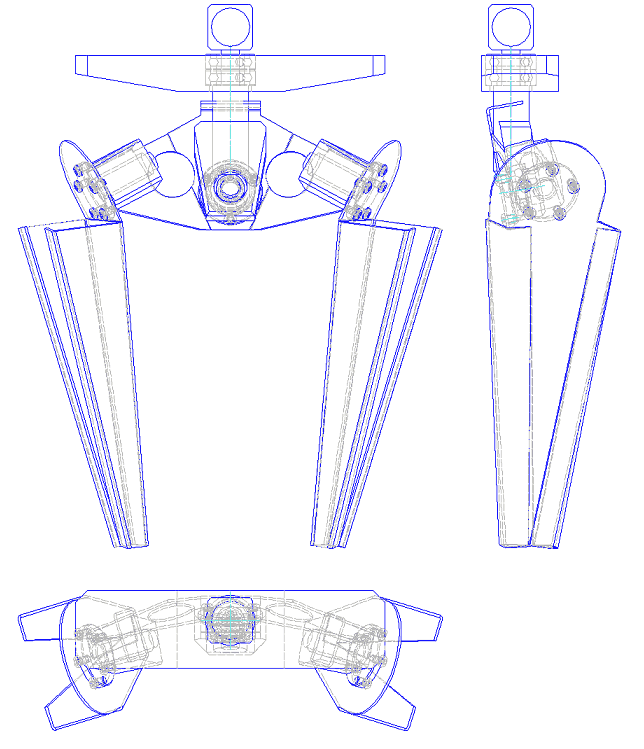
Quiero comentarles que estuve haciendo respecto al tema de la cadera:
Trabaje un poco en el ultimo modelo, pero me di cuenta que en la combinacion de angulos hay movimientos raros y queria comprenderlos. claro que es mas facil hacer una cadera fija y compensar el movimiento pendular en otro lado, pero...
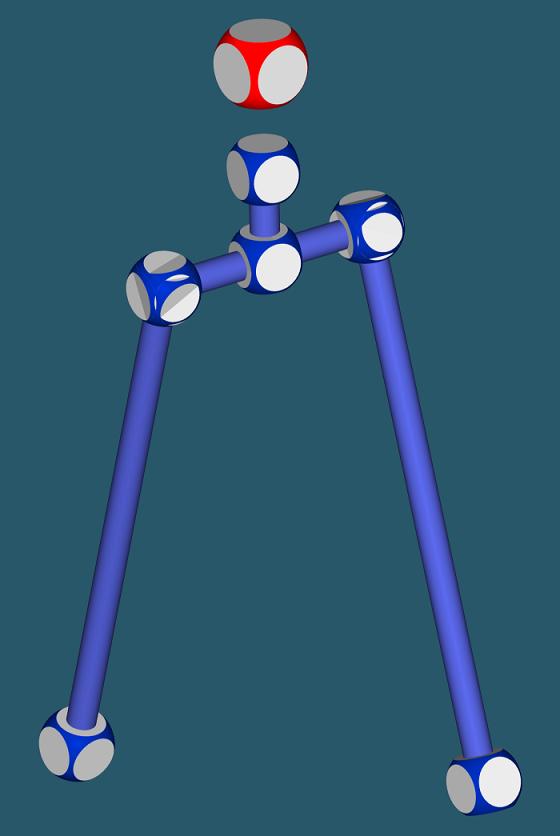
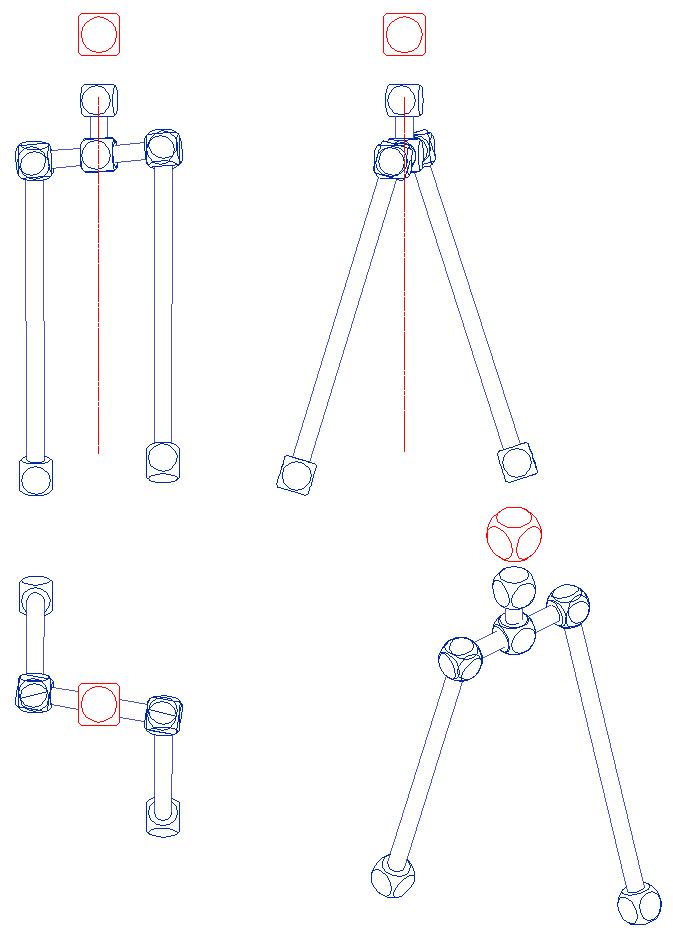
hice un modelo mucho mas simple, el que ven, tiene cada extremo unido a una esfera facetada, todos los puntos siempre se mantienen unidos y solo puedo variar los angulos, entre las partes, lo interesante es que el modelo esta con variables, unidas a una planilla de excel, puedo combinar secuencias de angulos y obtener la posicion de los puntos e incluso del cg en todos los casos.
tambien probe una "variacion" de angulos con una funcion seno como creo que se da cuando caminamos
continua..
--Mastromec 17:49 25 abr 2008 (ART)
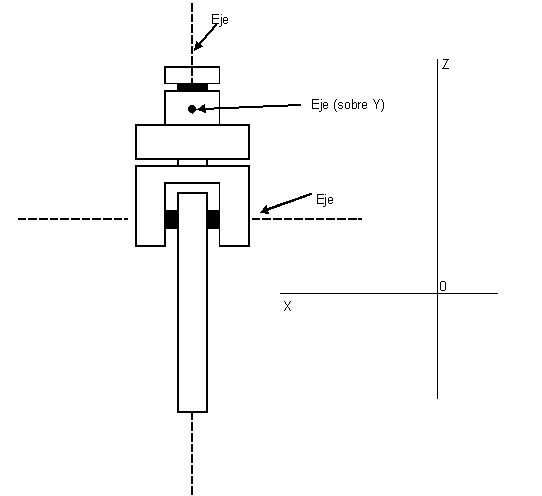
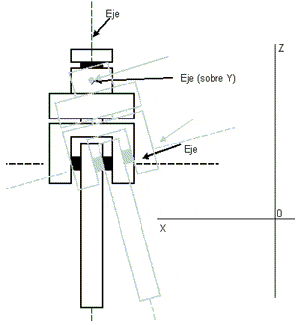
Hola, aquí Edu. ¿Los círculos indican --su centro-- un punto de giro, verdad? Ayudame con esto, que para mecánica e interpretación de planos no soy muy bueno...
--Edu 22:38 25 abr 2008 (ART)
Relacionados:
- Piernas
- Caderas
- Rodillas
- Tibias
- Pies
- Articulaciones
- Articulación de cadera
- Articulación de rodilla
- Articulación del pie